La magia de pensar con números: bate a tu inteligencia resolviendo este reto matemático, (7 + 3) × 2² - 4 + 6 ÷ 3

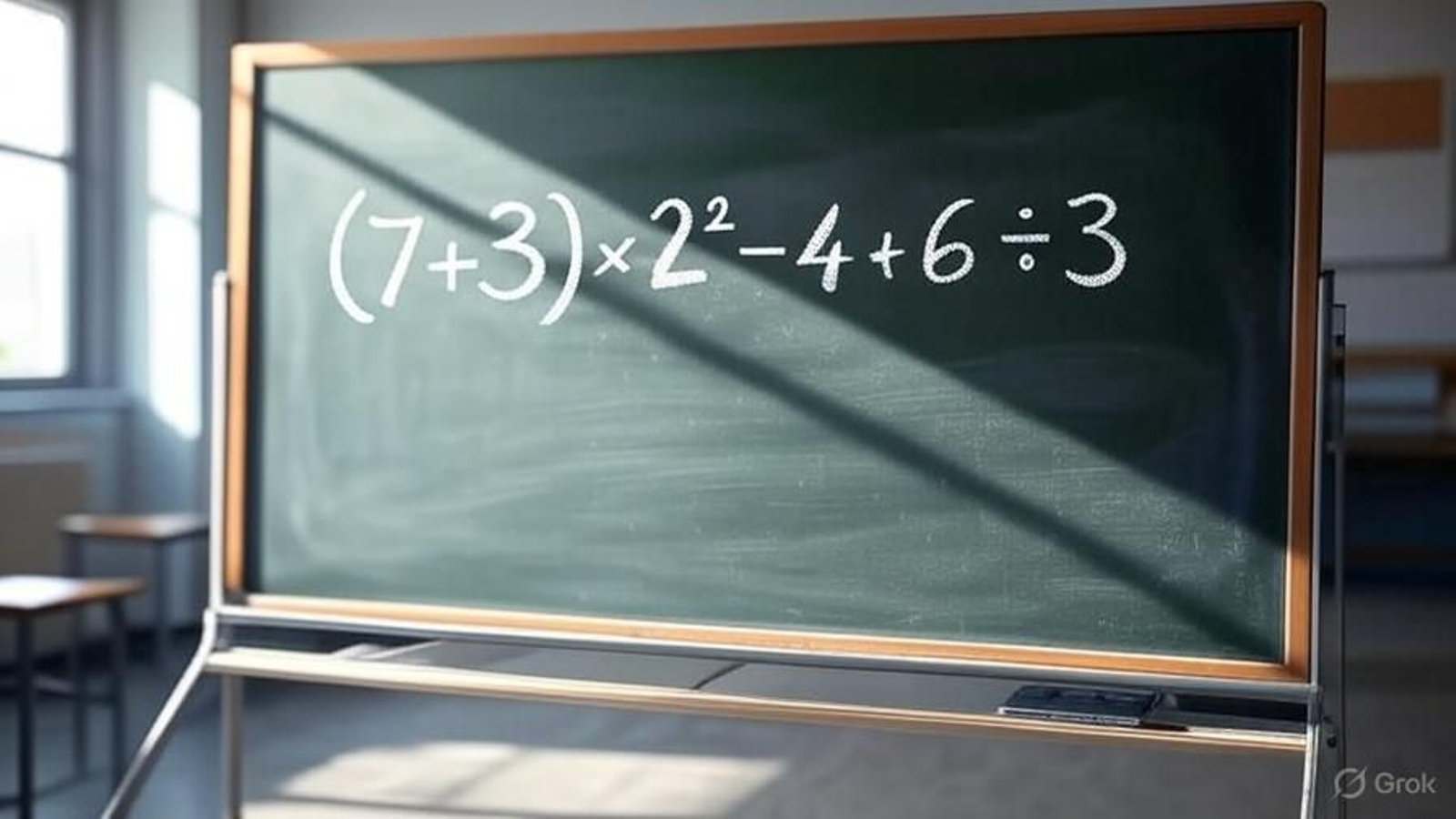
La palabra "matemáticas" suele despertar reacciones encontradas. Para algunos, es sinónimo de belleza, lógica y precisión; para otros, un recuerdo borroso de exámenes de fracciones, raíces cuadradas y fórmulas que parecían diseñadas para confundir. Pero lo cierto es que las matemáticas están presentes en casi todo lo que hacemos, queramos o no. Son el lenguaje invisible del universo, el código que da forma al mundo físico, a la tecnología que usamos y a las decisiones que tomamos a diario.

Desde el momento en que nos despertamos y miramos el reloj, hasta que apagamos las luces al final del día, estamos aplicando, consciente o inconscientemente, principios matemáticos. Al planificar el tiempo, calcular cuánto combustible necesita nuestro coche, repartir la comida en porciones iguales o estimar si una oferta del supermercado realmente conviene, estamos haciendo uso de operaciones aritméticas y de razonamiento lógico. En todas esas pequeñas decisiones, las matemáticas nos guían como una brújula racional.

Pero para que estas herramientas sean realmente útiles, es necesario entenderlas bien. Por eso existe un principio fundamental para resolver operaciones combinadas sin errores: el orden correcto de las operaciones. En inglés, la regla se conoce como PEMDAS, un acrónimo que resume los pasos: Paréntesis, Exponentes, Multiplicación y División, y finalmente Adición y Sustracción. En español, también se utiliza la regla PAPOMUDAS, con una estructura similar. Esta jerarquía de operaciones es más que una convención: es una norma universal que, si se ignora, conduce inevitablemente a resultados erróneos.

Pero antes de sumergirnos en la lógica de PEMDAS, conviene hacer una pausa y mirar hacia atrás. La historia de las matemáticas es una de las más fascinantes del saber humano. Surgieron no como entretenimiento intelectual, sino como necesidad vital. Las primeras civilizaciones necesitaban medir, contar, construir. Así, en la antigua Mesopotamia, se desarrollaron las primeras tablas de multiplicar en tablillas de arcilla. En Egipto, los escribas usaban reglas geométricas para construir pirámides con una precisión que sigue asombrando.

En Grecia, las matemáticas se convirtieron en filosofía. Pitágoras, Platón, Euclides… pensaban que el universo podía explicarse con proporciones numéricas. Mientras tanto, en la India se introducía el concepto revolucionario del cero, y en China se resolvían ecuaciones complejas con varillas de bambú. Más tarde, el mundo islámico expandió el conocimiento con avances fundamentales en álgebra, trigonometría y cálculo.

Los números, lejos de ser fríos, narran historias de comercio, navegación, arquitectura, arte, astronomía y hasta poesía. Los algoritmos que hoy gobiernan las redes sociales o la inteligencia artificial tienen su origen en manuscritos árabes del siglo IX. En definitiva, entender matemáticas es entender parte de lo que somos.

Y sin embargo, en la era digital, la dependencia de calculadoras y asistentes virtuales ha hecho que muchas personas pierdan agilidad para hacer operaciones básicas. Por eso, retomar la práctica de resolver desafíos matemáticos, incluso sencillos, tiene un valor enorme. No se trata solo de "saber cuentas", sino de ejercitar la mente, de aprender a seguir un orden, a tener paciencia y a verificar resultados. Las matemáticas enseñan algo más importante que números: enseñan rigor, método, precisión y disciplina mental.

Este artículo no solo te propone resolver ejercicios. Es una invitación a reconciliarte con el pensamiento matemático. A redescubrir, paso a paso, cómo resolver con claridad lo que parece complicado. Y a entrenar tu lógica con ejemplos reales, aplicables y desafiantes, bajo la guía infalible de una estructura milenaria.

Porque pensar en matemático no es solo resolver problemas: es vivir con claridad.

Cómo funciona PEMDAS: el orden de las operaciones

Cuando una operación contiene varios signos, no se puede resolver al azar. La regla PEMDAS establece el siguiente orden jerárquico para obtener el resultado correcto:

1. Paréntesis: todo lo que esté dentro de paréntesis se resuelve primero.
2. Exponentes: potencias o raíces.
3. Multiplicación y División: se resuelven en el orden en que aparecen, de izquierda a derecha.
4. Adición y Sustracción: también de izquierda a derecha.

Ejemplo clásico del error común:

¿Cuánto es 5 + 3 × 2?

Mucha gente responde 16, pero el resultado correcto es 11, porque se multiplica primero:

3 × 2 = 6 → 5 + 6 = 11.

Este principio se convierte en una herramienta poderosa cuando se enfrentan operaciones complejas, tanto en exámenes como en la vida diaria.

Cinco ejercicios resueltos paso a paso

Ejercicio 1

(7 + 3) × 2² - 4 + 6 ÷ 3

→ Paréntesis: 10

→ Exponente: 2² = 4

→ Multiplicación: 10 × 4 = 40

→ División: 6 ÷ 3 = 2

→ Suma y resta: 40 - 4 + 2 = 38

Ejercicio 2

12 × (5 - 2) + 9 ÷ (3 × 1)

→ Paréntesis: 5 - 2 = 3 y 3 × 1 = 3

→ Multiplicación: 12 × 3 = 36

→ División: 9 ÷ 3 = 3

→ Suma final: 36 + 3 = 39

Ejercicio 3

(18 ÷ 3 + 2) × (4 - 1)²

→ Paréntesis izquierdo: 18 ÷ 3 = 6 → 6 + 2 = 8

→ Paréntesis derecho: 4 - 1 = 3 → 3² = 9

→ Multiplicación: 8 × 9 = 72

Ejercicio 4

8 × [2 + (3² - 2)] - 5

→ Exponente: 3² = 9

→ Paréntesis interior: 9 - 2 = 7

→ Suma: 2 + 7 = 9

→ Multiplicación: 8 × 9 = 72

→ Resta: 72 - 5 = 67

Ejercicio 5

(6 + 4)² ÷ 2 - 3 × (2 + 1)

→ Paréntesis: 6 + 4 = 10 → 2 + 1 = 3

→ Exponente: 10² = 100

→ División: 100 ÷ 2 = 50

→ Multiplicación: 3 × 3 = 9

→ Resta: 50 - 9 = 41

Conclusión: pensar como matemático es pensar mejor

Las matemáticas no son solo una disciplina académica; son una forma de mirar el mundo con estructura, coherencia y claridad. Vivimos tiempos en los que la sobrecarga informativa exige tomar decisiones rápidas, interpretar datos, comparar cifras, planificar recursos. Todo eso es, en esencia, pensamiento matemático.

Aprender a resolver problemas con orden —siguiendo reglas como PEMDAS— fortalece habilidades que van mucho más allá del aula. Mejora nuestra capacidad para razonar bajo presión, detectar errores, analizar situaciones complejas y encontrar soluciones. En una sociedad dominada por la información y la inmediatez, quienes piensan con lógica y precisión tienen una ventaja competitiva.

Además, practicar matemáticas nos conecta con una historia de miles de años, en la que grandes mentes buscaron entender el universo a través del número. Hoy, ese mismo lenguaje nos permite programar ordenadores, modelar pandemias, diseñar edificios o prever crisis económicas.

Por eso, este reportaje no es solo un homenaje al orden de las operaciones, sino una defensa del pensamiento claro, estructurado y racional. Resolver problemas no es una cuestión de suerte, sino de método. Y en un mundo cada vez más complejo, pensar con método es más necesario que nunca.

Así que la próxima vez que veas una operación como "6 + 2 × (3 + 4)²", no huyas. Míralo como un pequeño reto, una oportunidad para poner tu mente en marcha. Porque cuando aprendes a dominar los números, no solo resuelves problemas… también entiendes mejor la vida.